Copyright FVP 2016
made with Brackets
made with Brackets
Versión 1.0 - Beta
El objetivo de esta web es el de ayudar al estudiante con el repaso de la materia vista en clases, de ninguna manera este apunte reemplaza la clase ni tampoco pretende tener todo el contenido visto.
Si tiene observaciones o dudas sobre la materia presentada en esta web, no dude en contactar al profesor o al ayudante.
Esta página ha sido creada este semestre como versión Beta, por lo que se espera que se comprendan problemas de visualización y falta de contenido.Esta sección pretende resumir los contenidos básicos que el alumno debe dominar para cursar el ramo.
$$\Rightarrow \sum P_{+} + \sum P_{-} = 0$$
$$V_{AB} = V_{AC}\cdot\frac{Z_1}{Z_1 + Z_2} \qquad V_{BC} = V_{AC}\cdot\frac{Z_2}{Z_1 + Z_2}$$
$$I_2 = I_1\cdot\frac{Z_3}{Z_3 + Z_2} \qquad I_3 = I_1\cdot\frac{Z_2}{Z_3 + Z_2}$$
$V_{rms}=\sqrt{ {1 \over T}\int_0^T{v^2(t)dt} }$
Si la señal es una sinusoide:
$v=A\cos{(\omega t)}$ $\Rightarrow v_{rms}={A \over \sqrt{2}}$
En este capítulo se analizarán redes de excitación sinusoidal, en particular en estado estacionario. Para esto es fundamental recordar el análisis fasorial y sus propiedades.
Un fasor es una representación polar de un voltaje o una corriente alterna, que pertenece al conjunto de los números Complejos $\mathbb{C}$ y cuya velocidad de rotación es $\omega$$=2\pi f$
:
En la Animación se aprecian dos fasores cuya proyección al eje horizontal generan dos sinusoides desfasadas, este desfase es exactamente el mismo que tienen los fasores. Si expresaramos la situación geométrica con ecuaciones y considerando los radios de los círculos como $A_1$ y $A_2$ para $y_1$ e $y_2$ respectivamente, podríamos definir:
$Y_1(r,\theta)$ : Fasor asociado a $y_1(t)$, con:
$r=|Y_1|$ $=A_1=cte.$ $\quad$ $\theta = \omega t + \phi_1$
$Y_2(r,\theta)$ : Fasor asociado a $y_2(t)$, con:
$r=|Y_2|$ $=A_2=cte.$ $\quad$ $\theta = \omega t + \phi_2$
Luego y tomando en cuenta que $\omega$ es constante, el eje vertical es imaginario $(\mathbb{Im})$ y el eje horizontal es real $(\mathbb{Re})$:
$Y_1(r,\theta)=|Y_1|[\cos(\omega t +\phi_1)+j\sin(\omega t +\phi_1)]$ $=|Y_1|e^{j(\omega t + \phi_1)}$ $=A_1 e^{j(\omega t + \phi_1)}$ $=A_1 e^{j \omega t}e^{j\phi_1}$
$Y_2(r,\theta)=|Y_2|[\cos(\omega t +\phi_2)+j\sin(\omega t +\phi_2)]$ $=|Y_2|e^{j(\omega t + \phi_2)}$ $=A_2 e^{j \omega t}e^{j\phi_2}$
Se define entonces como transformada fasorial:
$Y_1=P\{y_1\}$ $=A_1e^{j\phi_1}$
Cuya abreviación polar se escribe como:
$Y_1=A_1$$\phi_1$
Esta representación tiene un módulo y un ángulo pero no debe olvidarse que existe una rotación angular asociada al fasor, por lo que sólo pueden operarse fasores que roten con la misma frecuencia angular $\omega$.
De la misma forma se puede definir la transformación inversa de un fasor como:
$P^{-1}\{Y_1\}=\mathbb{Re}\{Y_1\}$ $=A_1 \cos{(\omega t + \phi_1)}$ $=y_1(t)$
$P^{-1}\{Y_2\}=\mathbb{Re}\{Y_2\}$ $=A_2 \cos{(\omega t + \phi_2)}$ $=y_2(t)$
Existe una definición de transformada fasorial basada en los valores efectivos de las señales sinusoidales, esta se define como:
$P\{A\cos{(\omega t + \phi)} \}={A \over \sqrt{2}}$$\phi$
La ventaja que tiene esta transformación es la de simplificar el cálculo de la potencia.
Un sistema lineal e invariante en el tiempo (LIT) excitado con un fuente sinusoidal presentará una respuesta separada en dos etapas:
El análisis fasorial sirve para analizar SOLO EL ESTADO ESTACIONARIO y solo puede operar fasores que roten a la misma velocidad, es decir, la misma frecuencia angular $\omega$.
Para analizar múltiples excitaciones sinusoidales con velocidades angulares distintas, se debe aplicar el principio de superposición, que es válido para sistemas LIT.
Si $\mathbb{A}=A$$\alpha$ y $\mathbb{B}=B$$\beta$ son dos fasores con el mismo $\omega$
Nota 1: La división da como resultado un número complejo y no otro fasor.
Nota 2: La multiplicación da como resultado un fasor del doble de la frecuencia.
La impedancia y admitancia se definen como la relación entre el voltaje y la corriente:
$$Z(\omega)={\mathbb{V} \over \mathbb{I} }$$
$$Y(\omega)={\mathbb{I} \over \mathbb{V}}$$
Como se puede apreciar dependen de la frecuencia angular $\omega$ de las señales, pero NO SON FASORES son una factor polar que no representa una rotación, solo un desfase angular y una transformación de magnitud.
Una Impedancia y Admitancia podrán tener parte real y parte imaginaria:
$$Z(\omega) = R + jX(\omega)$$ $$R: Resistencia$$ $$X(\omega): Reactancia$$
$$Y(\omega) = G + jB(\omega)$$ $$G: Conductancia$$ $$B(\omega): Susceptancia$$
Las Impedancias L y C son denominadas Reactivas debido a que solo poseen reactancia, mientras que las resistencias solo tienen parte resistiva.
La potencia instantánea se define como:
$$p(t) = v(t)i(t)=V\cos{(\omega t + \phi_v)}\cdot I\cos{(\omega t + \phi_i)}[W]$$
$\Leftrightarrow {VI \over 2} \lgroup \cos{(2\omega t + \phi_v + \phi_i)} + \cos{(\phi_v - \phi_i)} \rgroup$ $\Leftrightarrow {VI \over 2} \cos{(2\omega t + \phi_v + \phi_i)} + {VI \over 2} \cos{(\Delta\phi)}$
La cual posee una parte constante que no depente del tiempo llamada potencia media o activa
y una parte que depende del tiempo llamada potencia fluctuante
. La potencia activa o media es la que se disipa en los elementos resistivos, mientras que en los elementos reactivos no hay pérdidas, sólo acumulación de energía.
Si se quisiera cuantificar la potencia media acumulada por los elementos reactivos bastaría con desfasar el voltaje en $\pi/2$, dado que la parte reactiva de las cargas es ortogonal a la resistiva:
$$q(t) = v'(t)i(t)=V\cos{(\omega t + \phi_v - \pi/2)}\cdot I\cos{(\omega t + \phi_i)}[VAR]$$
$\Leftrightarrow {VI \over 2} \lgroup \cos{(2\omega t + \phi_v + \phi_i - \pi/2)} + \cos{(\phi_v - \phi_i - \pi/2)} \rgroup$ $\Leftrightarrow {VI \over 2} \sin{(2\omega t + \phi_v + \phi_i)} + {VI \over 2} \sin{(\Delta\phi)}$
Las potencias fluctuantes son traspasos de energía de cargas a fuentes y viceversa.
Después del análisis previo se puede concluir que existe una potencia compleja cuya parte real es ACTIVA y su parte imaginaria es REACTIVA, además su magnitud es ${VI \over 2}$ y su ángulo es $\Delta\phi=\phi_v-\phi_i$. Esta potencia es llamada potencia aparente y se mide en Volt Ampere $[VA]$.
$S = {VI \over 2}$$\Delta\phi$ $= {VI \over 2}$$\phi_v-\phi_i$ $=P + jQ$
La potencia activa es entonces $P[W]$ y la reactiva es $Q[VAR]$.
Usando la transformada fasorial, la expresión anterior debiera expresarse como:
$S={1 \over 2}\mathbb{V}\cdot \mathbb{I}^*=\frac{VI}{2}$$\phi_v - \phi_i$
Si los móduos de la transformación se definen como valores efectivos, entonces:
$S=\mathbb{V}\cdot \mathbb{I}^*=\frac{V}{\sqrt{2}}\frac{I}{\sqrt{2}}$$\phi_v - \phi_i$
Para ambos casos el resultado será el mismo. Por otro lado a potencia fluctuante se podría expresar como fasor:
$P_{fluc}={VI \over 2} [ \cos{(2\omega t + \phi_v + \phi_i)} + j\sin{(2\omega t + \phi_v + \phi_i)} ]$
Notar que este fasor no tiene la misma frecuencia angular que el votaje y la corriente, si no que el doble.
Son redes conformadas por dos o mas fuentes sinusoidales (FASES). Generalmente están desfasadas de forma equilibrada, de modo que la suma total de ellas sea siempre cero.
$V_k = V$${2\pi k \over m}$ , con $k=1,2,..,m$ $\quad m\geq 3$
...es un sistema de producción, distribución y consumo de energía eléctrica formado por tres corrientes alternas monofásicas de igual frecuencia y amplitud (y por consiguiente, valor eficaz) que presentan una cierta diferencia de fase entre ellas, en torno a 120°, y están dadas en un orden determinado. Cada una de las corrientes monofásicas que forman el sistema se designa con el nombre de fase.
-wikipedia-
En la figura las tres sinusoidales sumadas tienen resultado nulo para todo tiempo, pero ¿Como se distribuye y conecta una red trifásica?
La distribución en estrella consiste en distribuir tres fases unidas en un punto llamado NEUTRO
Donde (usando grados sexagesimales):
$V_{an} = V_{\phi}$$0°$
$V_{bn} = V_{\phi}$$-120°$
$V_{cn} = V_{\phi}$$120°$
En secuencia a-b-c
$V_{an} = V_{\phi}$$0°$
$V_{bn} = V_{\phi}$$120°$
$V_{cn} = V_{\phi}$$-120°$
En secuencia c-b-a
Se puede calcular la diferencia de potencial entre dos voltajes de fase, este voltaje se llama voltaje entre líneas:
$V_{ab}=V_{an}-V_{bn}$ $=V_{\phi}[\cos{(0)}+j\sin{(0)}-\cos{(-120)} -j\sin{(-120)}]$ $=V_{\phi}[{3 \over 2} + j{\sqrt{3} \over 2}]$ $=V_{\phi} \sqrt{3}$$30°$ $=V_{an} \sqrt{3}$$30°$
De la misma forma se pueden encontrar las siguientes relaciones:
$$V_{bc}=V_{bn}-V_{cn}$$ $=V_{bn} \sqrt{3}$$30°$
$$V_{ca}=V_{cn}-V_{an}$$ $=V_{cn} \sqrt{3}$$30°$
Siempre que el sistema tenga voltajes de amplitud igual y fases de $120°$ entre ellas, se dice que el sistema de distribución es simétrico o balanceado.
La distribución en forma de estrella requiere de cuatro cables, las tres fases y un neutro. En los sistemas de distribución de baja potencia en Chile las tensiones por fase son de $220[V]$ efectivos o RMS y los voltajes de línea son $220\sqrt{3}[V]$ $=380[V]$.
La distribución eléctrica en forma delta une en serie las tres fases y no requiere de un neutro
En este caso los voltajes de cada fase son equivalentes a los voltajes de línea y se mantienen los desfases de $120°$ entre cada línea. Una ventaja de esta modalidad de distribución es que no requiere de un neutro.
$V_{l-l} = \lVert \mathbb{V}_{ab} \rVert = \lVert \mathbb{V}_{bc} \rVert = \lVert \mathbb{V}_{ca} \rVert$
$V_{ab}=V_{l-l}$$\alpha$$\quad$ $V_{bc}=V_{l-l}$ $\alpha-120°$$\quad$ $V_{ca}=V_{l-l}$$\alpha + 120°$
Una buena estrategia de distribución es la de elevar las tensiones de distribución para disminuir el valor de corriente y así disminuir las pérdidas por disipación resistiva: $I^2R$
En la siguiente imágen se pueden ver los voltajes usados en américa latina
Ya se han visto las conexiones para las fuentes de voltaje, ahora se verán las conexiones de las cargas o impedancias.
Las cargas, al igual que las fuente se pueden conectar en estrella o delta. Se dice que la carga es balanceada cuando:
$Z_{AN}=Z_{BN}=Z_{CN}\quad$ $Z_{AB}=Z_{BC}=Z_{CA}$
Si tanto las fuentes como las cargas están balanceadas, no sería necesaria la conexión de un neutro, pero en la práctica las cargas no están siempre balanceadas.
Para la conexión Y-Y, la corriente por carga es igual a la corriente de línea y los voltajes de fase son los de las cargas.
$I_{A}={V_{AN} \over Z_{AN}}$ $\quad$ $I_{B}={V_{BN} \over Z_{BN}}$ $\quad$ $I_{C}={V_{CN} \over Z_{CN}}$
Si las cargas están balanceadas se pueden reemplazar por una de valor $Z$$\varphi$, y considerando secuencia directa con $V_{AN}=V_{\phi}$$0$:
$I_{A}={V_{\phi} \over Z}$$-\varphi$
$I_{B}={V_{\phi} \over Z}$$-120°-\varphi$
$I_{C}={V_{\phi} \over Z}$$120°-\varphi$
Para la conexión Δ-Δ, la tensión por carga es igual a la tensión de línea, entonces el cálculo de la corriente por carga es:
$I_{AB} = { V_{AB} \over Z_{AB} }$ $\quad$ $I_{BC} = { V_{BC} \over Z_{BC} }$ $\quad$ $I_{CA} = { V_{CA} \over Z_{CA} }$
Luego, si se requiere calcular la corriente de línea, por ejemplo en el nodo "A":
$I_A = I_{AB} - I_{CA}$ $= {V_{AB} \over Z_{AB}} - {V_{CA} \over Z_{CA}} $
Si las cargas están balanceadas se pueden reemplazar por una de valor $Z$$\varphi$, quedando:
$I_A = {V_l \over Z|\varphi}[1$$0°$$ - 1$$120°$$]$ $= {V_l \over Z}$ $-\varphi$$\cdot \sqrt{3}$$-30°$ $= I_{AB}\cdot \sqrt{3}$$-30°$
De la misma forma se puede comprobar que:
$I_B = I_{BC}\cdot \sqrt{3}$$-30°$
$I_C = I_{CA}\cdot \sqrt{3}$$-30°$
Contenido Pendiente
Contenido Pendiente
Contenido Pendiente
Los sistemas lineales presentan comportamientos transitorios, que en algunos casos suelen desvanecerse luego de un determinado tiempo y un comportamiento permanete, usualmente forzado por alguna entrada.
Los sistemas lineales cuyas entradas y salidas son acotadas (no tienden a infinito) se denominan sistemas lineales estables. En este curso se analizarán las respuestas transitorias y permanentes de Redes Eléctricas Lineales y Estables (que son un tipo de sistema lineal). La herramienta fundamental para hacer este estudió será la transformada de Laplace, la que permite resolver ecuaciones diferenciales mediante el uso de álgebra.
La transformada de laplace se puede usar para representar a señales y sistemas, y por ende se deben tener muy claras sus diferencias a la hora de utilizarla para el análisis de redes eléctricas.
La transformada de Laplace es un tipo de transformada integral frecuentemente usada para la resolución de ecuaciones diferenciales ordinarias. La transformada de Laplace de una función f(t) definida (en ecuaciones diferenciales, en análisis matemático o en análisis funcional) para todos los números positivos t ≥ 0, es la función F(s), definida por:
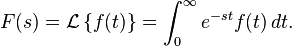-es.wikipedia.org-
Algunas transformadas relevantes para el curso:
| $f(t), t>0$ | $F(s)$ |
| $\delta(t)$ | $1$ |
| $1$ | ${1 \over s}$ |
| $\mu(t)$ | ${1 \over s}$ |
| $e^{-at}$ | ${1 \over {s+a}}$ |
| $cos(\omega t)$ | ${s \over {s^2+ \omega^2}}$ |
| $sen(\omega t)$ | ${\omega \over {s^2+ \omega^2}}$ |
| $f(t), t>0$ | $F(s)$ | Propiedad |
| $f(t-\tau)\mu(t-\tau)$ | $e^{-\tau s}F(s)$ | Desplazamiento temporal |
| $e^{-at}f(t)$ | $F(s+a)$ | Amortiguación exponencial |
| $af(t)+bg(t)$ | $aF(s)+bG(s)$ | Linealidad |
| ${df(t) \over dt}$ | $sF(s)-f(0^-)$ | Transformada de la derivada |
| $\int_0^t{f(t)dt}$ | $F(s) \over s$ | Transformada de la integral |
| $f(t),t\rightarrow 0$ | $\lim_{s \to \infty}sF(s)$ | Teorema del valor inicial |
| $f(t),t\rightarrow \infty$ | $\lim_{s \to 0}sF(s)$ | Teorema del valor final |
Como ejemplo, un sistema como el siguiente con excitación $u(t)$ y respuesta $y(t)$:
$\ddot{y}(t)+A\dot{y}(t)+By(t) = B\dot{u}(t)+Du(t)$
Tiene una representación en el "Plano de Laplace":
$[s^2Y(s)-sy(0^-)-\dot{y}(0^-)]$ $+A[sY(s)-y(0^-)]+BY(s)$ $= B[sU(s)-u(0^-)]+DU(s)$
$[s^2Y(s)+AsY(s)+BY(s)]$ $-[Ay(0^-)+sy(0^-)+\dot{y}(0^-)]$ $=BsU(s)+DU(s) - Bu(0^-)$
$Y(s)[s^2+As+B]$ $=U(s)[Bs+D]$ $+[(A+s)y(0^-)+\dot{y}(0^-)]$ $- Bu(0^-)$
$Y(s)$ $=U(s){[Bs+D] \over [s^2+As+B]}$ $+{ X_{ \langle u(0^-),y(0^-),\dot{y}(0^-) \rangle } \over [s^2+As+B] }$
$Y(s)$ $=U(s)H(s)$ $+{ 1 \over [s^2+As+B] } X_{ \langle u(0^-),y(0^-),\dot{y}(0^-) \rangle }$
Luego, la respuesta temporal del sistema en el tiempo se define como:
$y(t) = \mathscr{L}^{-1} \lbrace Y(s) \rbrace $ $, t > 0$
Una Red Pasiva tiene tres impedancias lineales conocidas: Resistencia, Inductor y Condensador.
NOTA: Recordar que el concepto de linealidad se aplica sólo a sistemas y no a señales y que significa que cumple con dos propiedades: Homogeneidad y Superposición
La ecuación de la resistencia (suponiendo invarianza en el tiempo y con respecto a la temperatura) es la siguiente:
$v(t)=R \cdot i(t) \Rightarrow \mathscr{L} \lbrace v(t) \rbrace = \mathscr{L} \lbrace R \cdot i(t) \rbrace $ $\Rightarrow V(s) = R \cdot I(s)$
$$ {V(s) \over I(s)} = R $$
Mientras que una carga puramente capacitiva tiene la siguiente ecuación diferencial:
$C{dv(t) \over dt}=i(t) \Rightarrow \mathscr{L} \lbrace C{dv(t) \over dt} \rbrace = \mathscr{L} \lbrace i(t) \rbrace$ $\Rightarrow C[sV(s)-v(0^-)] = I(s)$
$$ V(s) = {1 \over sC} \cdot I(s) + {v(0^-) \over s}$$
La ecuación diferencial de una carga inductiva es:
$v(t)=L{di(t) \over dt} \Rightarrow \mathscr{L} \lbrace v(t) \rbrace = \mathscr{L} \lbrace L{di(t) \over dt} \rbrace$ $\Rightarrow V(s) = L[sI(s) - i(0^-)]$
$$ V(s) = sL \cdot I(s) - Li(0^-)$$
En resumen:
$V(s) = R \cdot I(s)$
$V(s) = { 1 \over sC } \cdot I(s) + { v_0 \over s }$
$V(s) = sL \cdot I(s) - Li_0$
También se pueden expresar estas relaciones como modelo de admitancias, quedando:
$I(s) = {1 \over R} \cdot V(s)$
$I(s) = sC \cdot V(s) - Cv_0$
$I(s) = {1 \over sL} \cdot V(s) + {i_0 \over s}$
Entonces las impedancias C y L tienen un equivalente circuital como se muestra a continuación:
Se define como respuesta transitoria a la salida de un sistema que dura un breve período de tiempo, usualmente 4-5$\tau$, donde $\tau$ es la constante de tiempo asociada a la respuesta natural del sistema.
La respuesta permanente, también llamada respuesta estacionaria o estado estacionario (cuando se refiere al estado de la red o sistema lineal), es la respuesta que perdura en el tiempo luego de la respuesta transitoria y está relacionada con las entradas o posibles fuentes de voltaje o corriente internas.
A continuación se muestran las respuestas para distintos tipos de sistemas de segundo orden, todos forzados a una salida $y(t) = 1$
La respuesta transitoria se relaciona directamente con los modos naturales de una red, que para redes estables desaparecen. Mientras que el estado estacionario se relaciona con las entradas.
Del sistema propuesto con anterioridad, se llega a la siguiente expresión:
$Y(s)$ $=U(s){[bs+d] \over [s^2+as+b]}$ $+{ X_{ \langle u(0^-),y(0^-),\dot{y}(0^-) \rangle } \over [s^2+as+b] }$
Llamaremos al polinomio $A(s) = s^2+as+b$, como Polinomio Característico.
A la división: $H(s) = { {bs+d} \over {s^2+as+b}}$, la llamaremos Función de Transferencia
.
Se puede observar que la respuesta $y(t)$ puede encontrarse al transformar inversamente $Y(s)$. Si todos los sumandos de $Y(s)$ poseen el mismo denominador $A(s)$ la transformación inversa SIEMPRE incluirá un polinomio en el denominador.
Para analizar todas las posibles soluciones al calcular la transformada inversa de un polinomio en "s", se puede hacer la siguiente generalización:
Por lo anterior, el análisis de la salida en el tiempo se puede hacer por la superposición de todas las transformadas inversas de cada factor que aparece luego de las fracciones parciales.
Se pueden identificar tres tipos de polinomios:
Cada una de estas soluciones se denomina Modo Natural
, de forma que el orden del polinomio característico coincide con el número de modos naturales presentes en una red.
Las transformadas inversas que se pueden encontrar para cada uno de estos factores de las fracciones parciales son:
Finalmente la salida $y(t)$ será una combinación lineal de las posibles respuestas.
Si la entrada resulta ser un señal escalón o una sinusoide, lo esperable es que una vez agotado el tiempo transitorio, sean estas entradas las que permanezcan en el sistema, en este caso se habla de un modo forzado
. Esto sucede debido a que esta señal agrega un modo o raíz extra en denominador que no pertenece a sistema, y por ende la salida refleja este modo ajeno al sistema.
